The Special and General Theories of Relativity weren't just another discoveries, rather notions that re-thought the very existence of space and time. Although the topics are unintuitive, we can attempt to abstract them to visually understand what's happening. This article follows a narrative which covers topics ranging from the basics of unaccelerated reference frames of Special Relativity, to the distortions in spacetime of General Relativity.
The speed of light, 'c', is constant. Why?
Look at the visualisation on the right. Light is a
wave formed by alternating magnetic and
electric fields. It must move to exist. If its
speed were to vary, there would be a scenario
where you could perceive it to be stationary.
That's impossible, because the alternating
fields must constantly move, and never be
stationary. Thus, c is a constant.
This fact is important and forms the backbone
of what we encounter hereon.
Reference frames are different points of view through which events can be seen. The same event can be seen differently from different reference frames.
Consider two friends waving at each other. One is in a moving rocket with uniform linear motion (moving unaccelerated in a straight line), and the other outside. Notice how both friends can easily perceive themselves to be at rest, and the other one as moving.
Based on what we just saw, the restricted principle of relativity tells us that no reference frame is special. In other words, all reference frames must have the same laws of physics (for instance, the speed of light).
It's restricted, because at the moment we are only talking about uniformly and linearly moving reference frames.
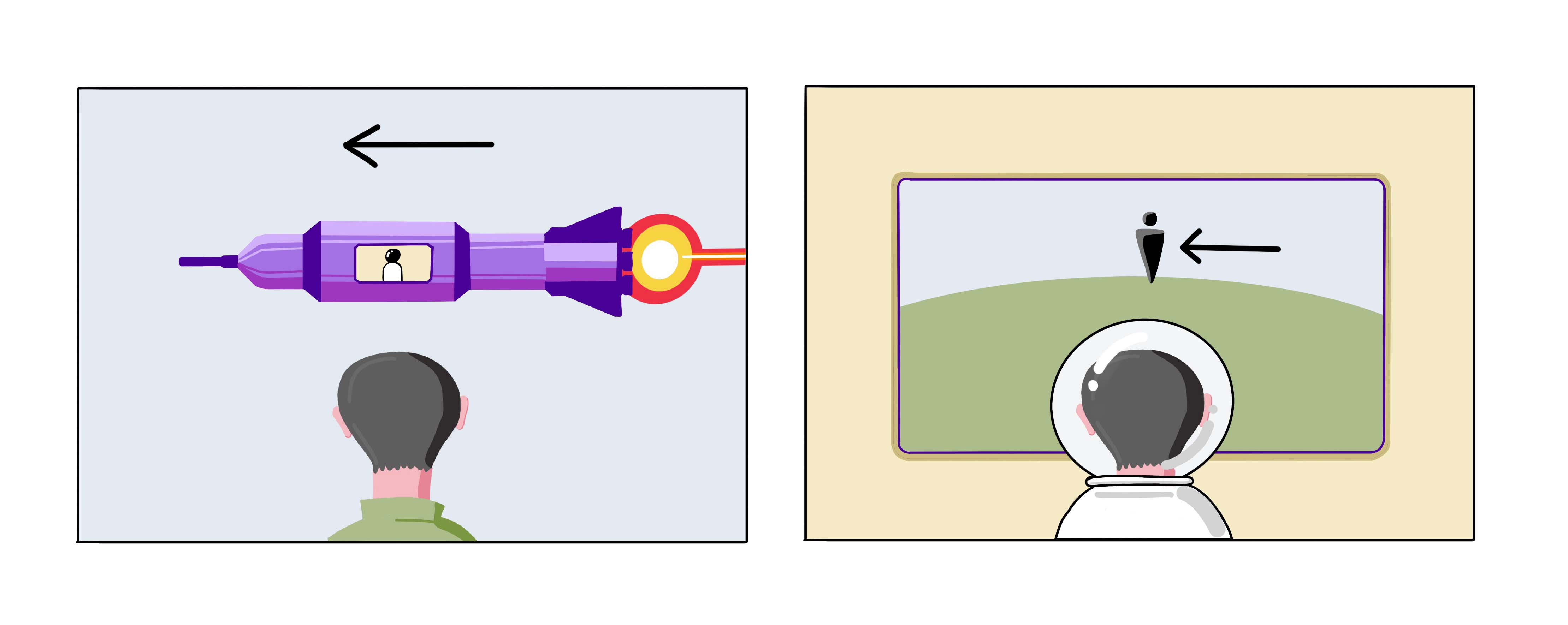
We just saw that no observer should measure light moving at a speed other than c. But, what if the friend in the spaceship lights up a torch? Will the speed of light add up with the spaceship’s speed for the outside observer?
The answer is it won’t. The speed has to remain constant, and for that, something has to give way. That something is time.
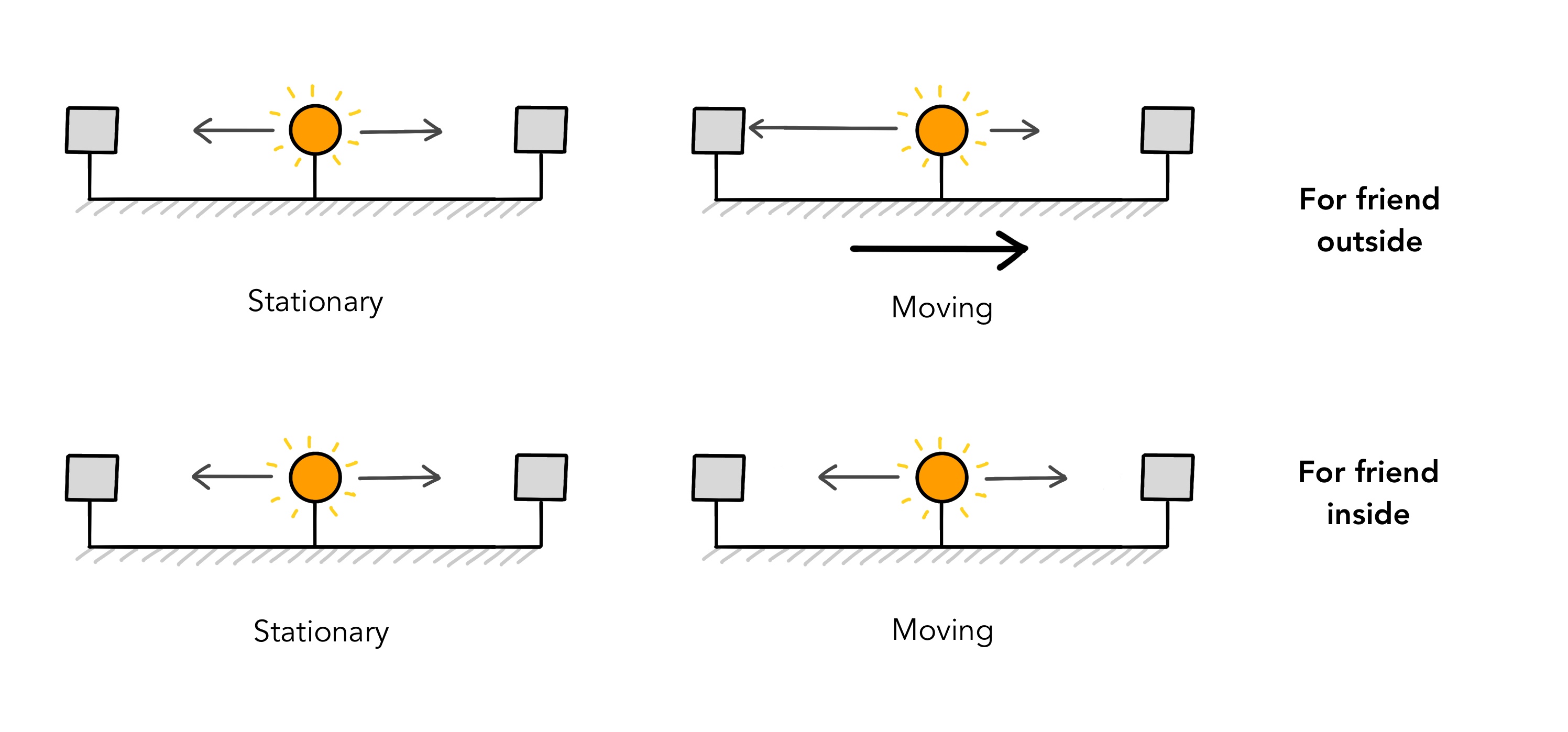
Consider the plank on the left, with a photon emitter (in easy words, a light torch) in the centre, and two mirrors at each end. Imagine it is kept in the spaceship of the friend we saw earlier.
If the ship is stationary, both friends see the photons hit the mirrors at the same time. Now, when the ship is moving at a constant velocity, as seen by the friend outside, light takes a longer time to reach the right mirror. This is because, after the light is emitted, the mirror on the right has moved further away, and light has to travel a greater distance.
On the other hand, the friend inside the spaceship sees the light hitting the two mirrors simultaneously, as the plank is at rest compared to him, and only the world outside his window is moving.
All objects, even stationary ones, are constantly moving through time, tirelessly progressing towards the future. Let's add a moving time direction on the Y axis on our plank visualisation.
Move the slider to change the ship's velocity. Once the velocity is something other than zero, it's clear how the event of the photons hitting both the mirrors is simultaneous for the friend on the spaceship, but not so much for the friend watching from outside.
This happens because, as the light is emitted, the two ends are at different positions in spacetime. Notice how, as the plank moves faster, its length also distorts. [1]
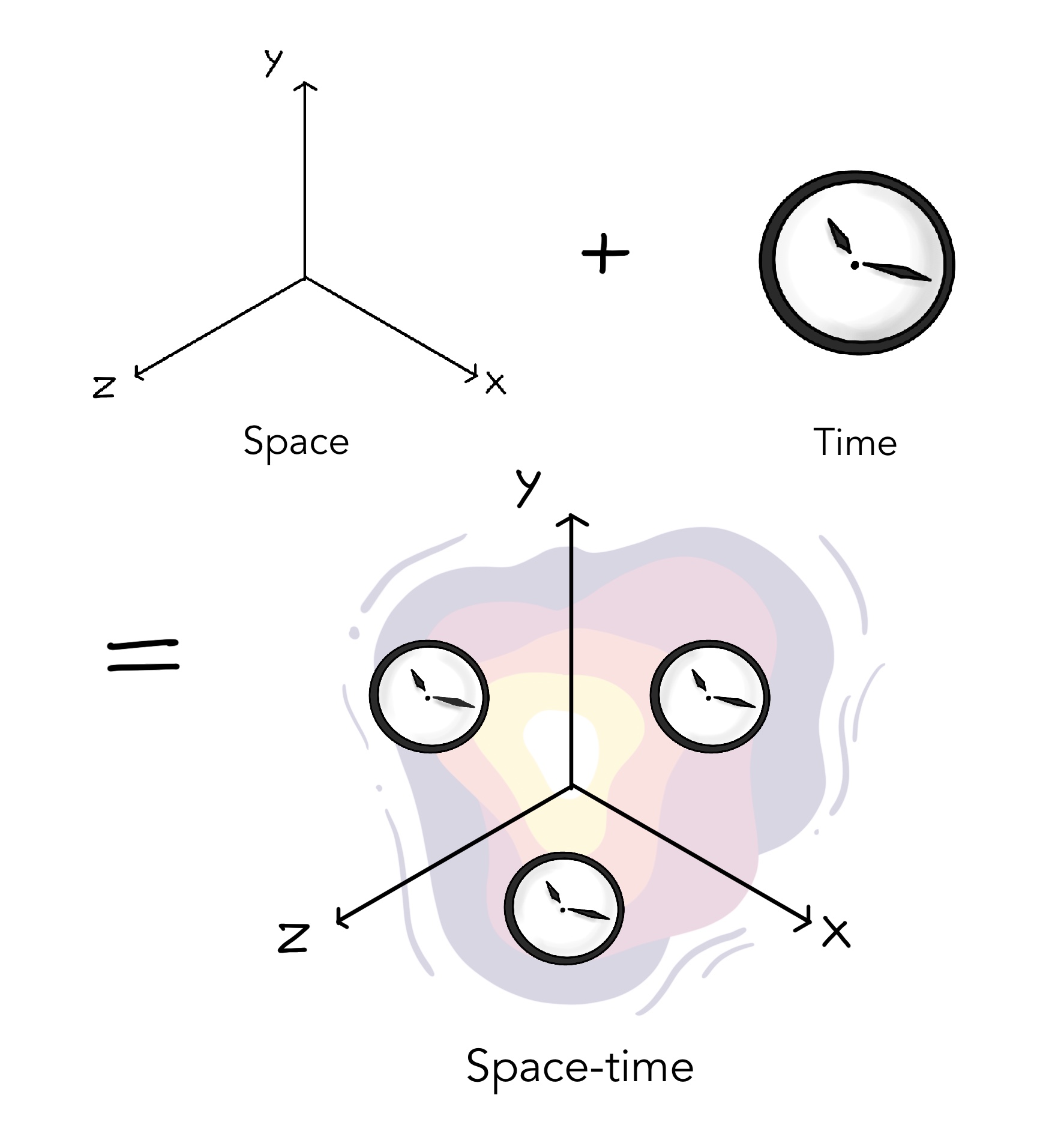
As seen from the previous visualisation, desynchronization in time is inevitably accompanied by length foreshortening. This leads us to the revolutionary suggestion by Einstein- Space and Time are not independent, but one. You can’t change one without affecting the other. Whenever you move, it’s never exclusively in space or time. It is ALWAYS in SPACETIME.
Since you are a 3 dimensional being watching this on a 2 dimensional screen, it is impossible for me to even try to visualise 4 dimensional spacetime. I will, however, extract some spatial dimensions in the visualisations that follow, and show them with time.
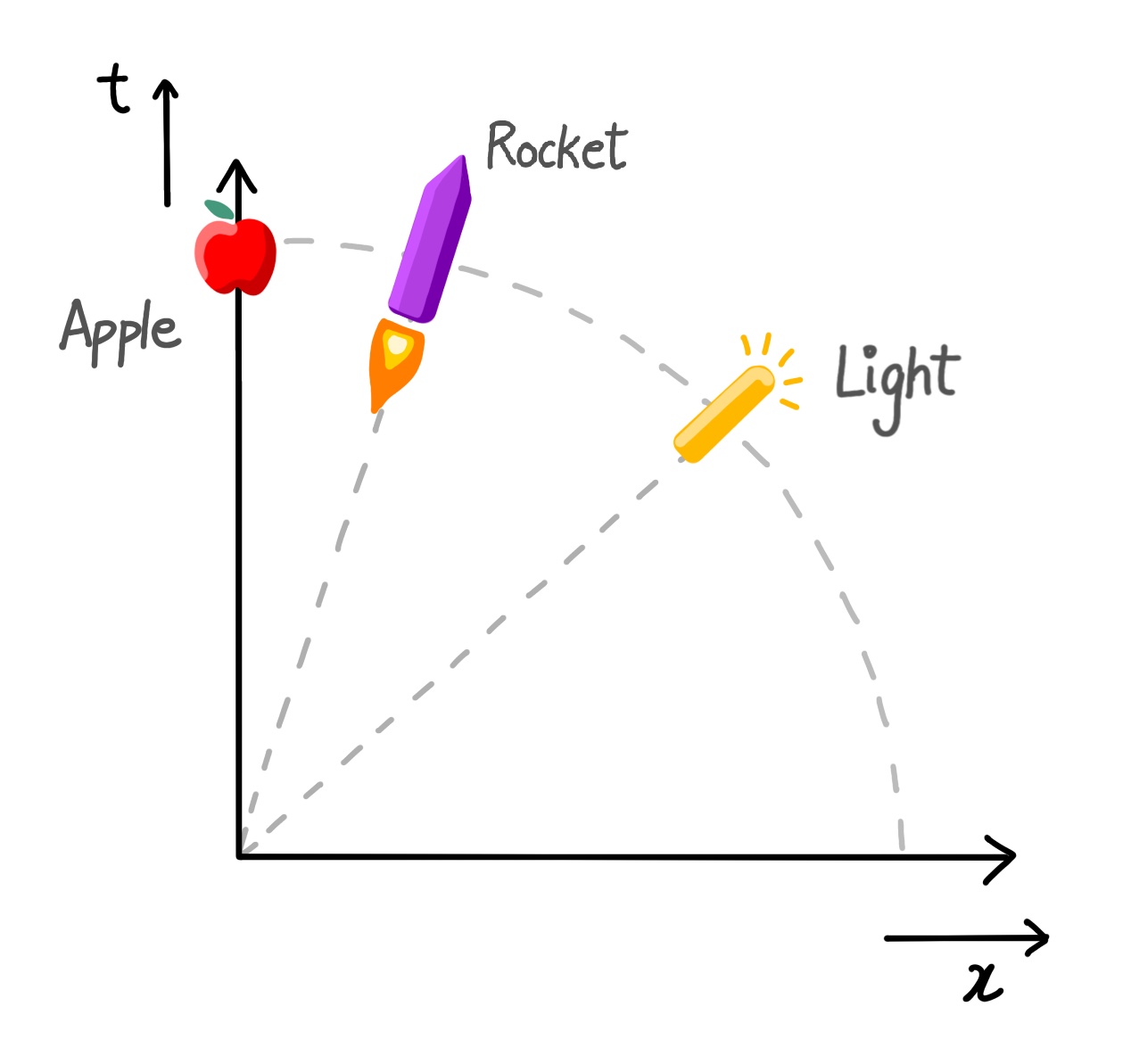
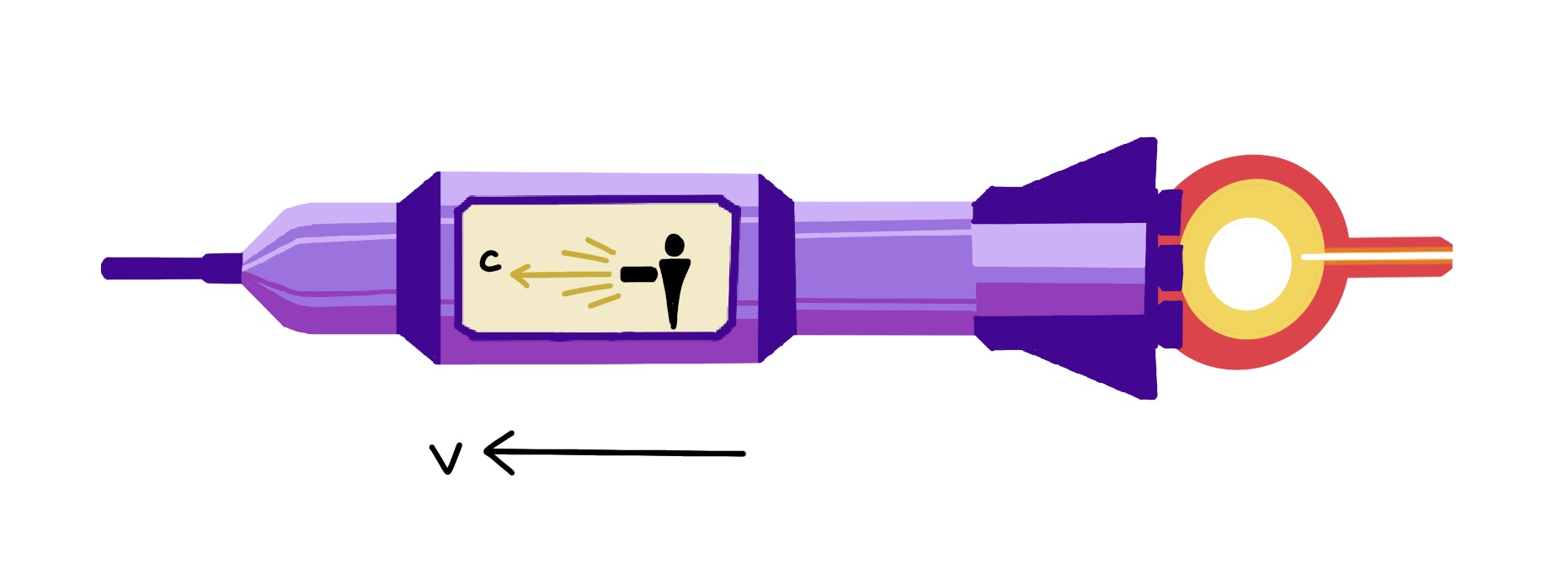
Here is where the “assumption” comes in: everything travels through spacetime at the speed of light c, nothing less and nothing more. Stars, planets, atoms, trees, me and you, all are ALWAYS hurling through spacetime at the maximum possible speed. Even stationary objects are moving through time, as space and time are not independent. [2]
If an object does move through space, it has to divert some of its speed through time to move through space. Thus, it moves through less time.
Why do fast moving objects move through less time? Consider a huge a photon tube (basically, a tube with a light torch), and place this on the spaceship of one of our two friends. The tube is 1 light second long (ie. light takes 1 second to reach from one end to another, if the tube is stationary). The left tube is from the frame of reference of the traveller, while the right one is as seen by the outsider.
From the point of emission at the origin, the photon can only reach the edge of the dotted arc in one second, since it has a fixed velocity. Push that gas pedal on the ship and notice that as the tube moves faster and faster, the photon is able to cover a lesser vertical distance. This leads to apparent length of the tube being shorter the faster it is moving (the foreshortening effect), and the tube itself appearing to travel slower in time.
Note that all this is from the reference frame of the outsider. The friend on the spaceship still views it to be stationary, as seen on the tube on the left. Also notice, as the speed of the tube approaches the speed of light, it stops moving through time, as the light can never reach the other point, and its size becomes zero due to both the end points coinciding.
Recall the banner visualisation on top of this page, showing a rocket hurling through space. If you moved the slider below it to change its speed, you'd have noticed that it shrinks the faster it is moving, as viewed by someone who is outside and stationary.
The 'speedometer' on the right helps visualise the exact length contraction and time dilation affecting the spaceship, which we get using formulae called Lorentz Transformations. The number next to 't' on the Y-axis is the fraction telling us exactly how much slower the spaceship is moving through time.
Remember that no reference frame is special: just as the friend outside sees the time slowing down on the spaceship and the length getting contracted, the traveller observes the same for the world outside, for he has no reason to
believe that he isn’t at rest and the world outside isn’t moving backwards.
A cosmic speedometer is easy to understand, but physicists prefer spacetime diagrams where velocity is represented by slope. These
diagrams show a single spatial dimension on one axis, and the time dimension on the other.
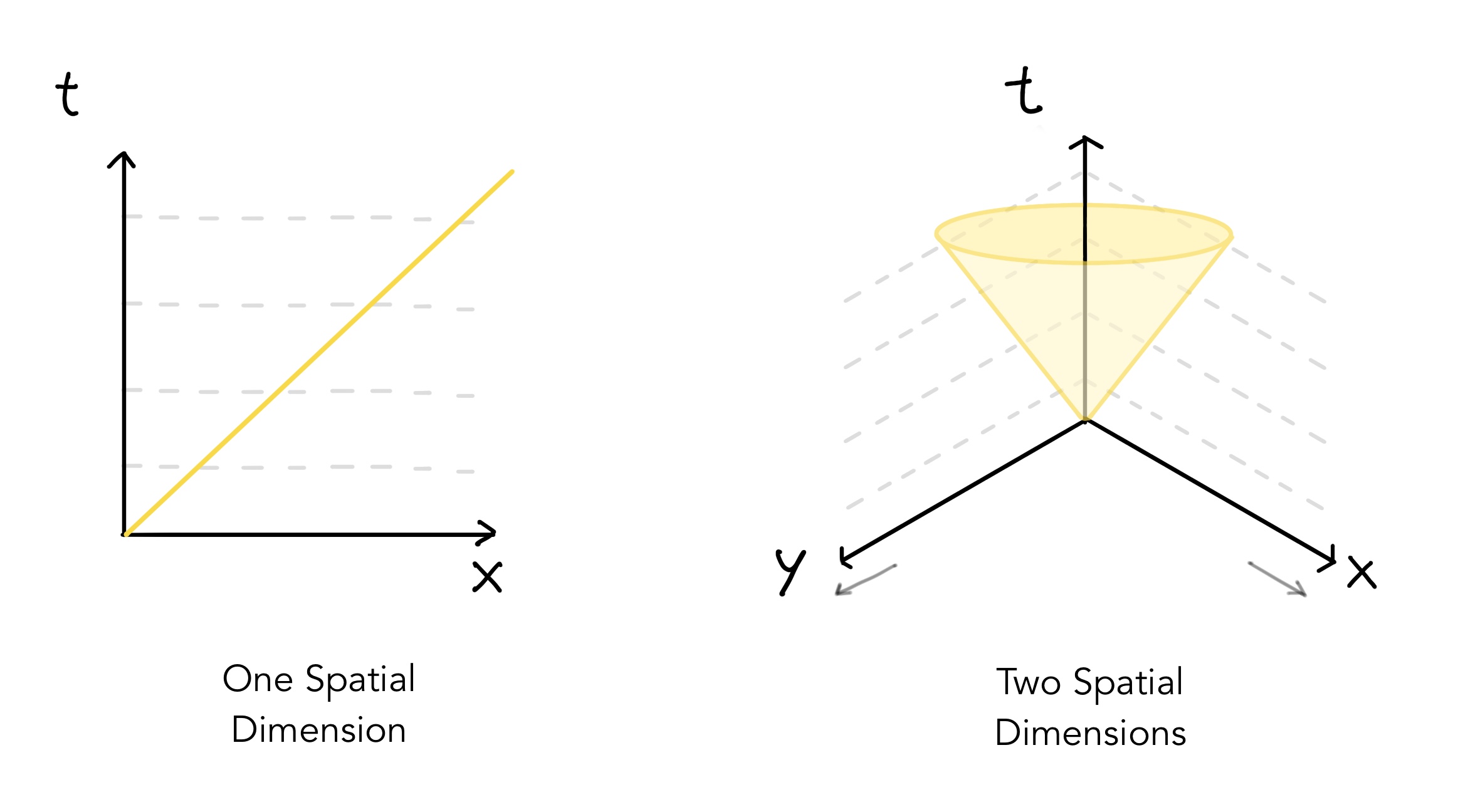
All objects follow a path on this diagram, depending on their speed through space, called their worldline. The spatial and temporal dimensions are chosen such that the world line of light is a 45 degree inclined line. If we include the Z axis to show another spatial dimension, we can extrude this 45 degree line to form a cone, called a light cone.
What would happen if our friend in the rocket ship decides to accelerate or turn his ship, while his friend outside doesn’t move? How would time and space behave for both of them?
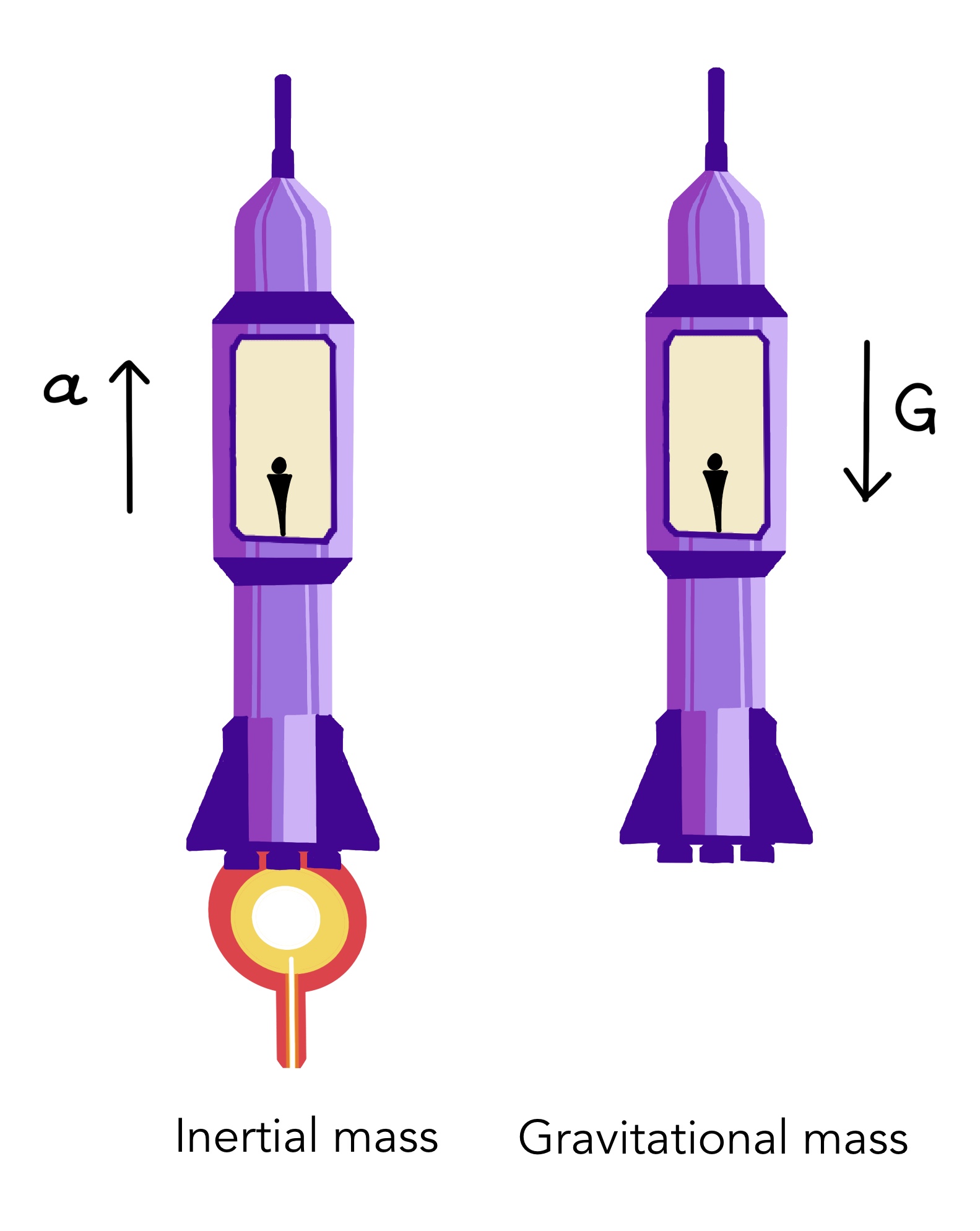
This leads us to Einstein's most beautiful thought, the Principle of Equivalence, which says that accelerating reference frames can be thought of as stationary if one believes that an external gravitational field is acting on the frame. This allows us to apply the principle of relativity, which we just discussed, in a more GENERAL sense, ie. all laws of physics hold true for such a reference frame, including the constancy of velocity of light.
The figure on the right gives us the following important insight, inertial mass = gravitational
mass
Taking a break from the two friends, consider a huge merry-go-round that is rotating around
its center. The rotational speed can be such that the outermost edge of the disc can almost but not completely reach the speed of light. Now, how would three different people, standing at blue, red and grey points, measure the circumference?
Move the slider to make the merry-go-round rotate. On a rotating disc, the outermost point is moving faster with respect to the points closer to the center, with the center always being stationary. Hence, according to our knowledge from Special relativity, the points moving faster should experience a slower clock. Also, the circumference of the disc should be measured differently by two observers who are at different distances from the center, due to relativistic length foreshortening, although the radius would be the same for everyone.
This clashes with our knowledge of classical geometry (or Euclidean geometry), where a circle of a fixed radius has to have a fixed circumference. This leads us to conclude that space and time don’t behave as expected when reference frames are accelerated. A straight line isn’t always straight, and triangles aren’t always planar. Think of it as a napkin. A line drawn on a flat napkin appears to curve if the napkin is wrinkled.
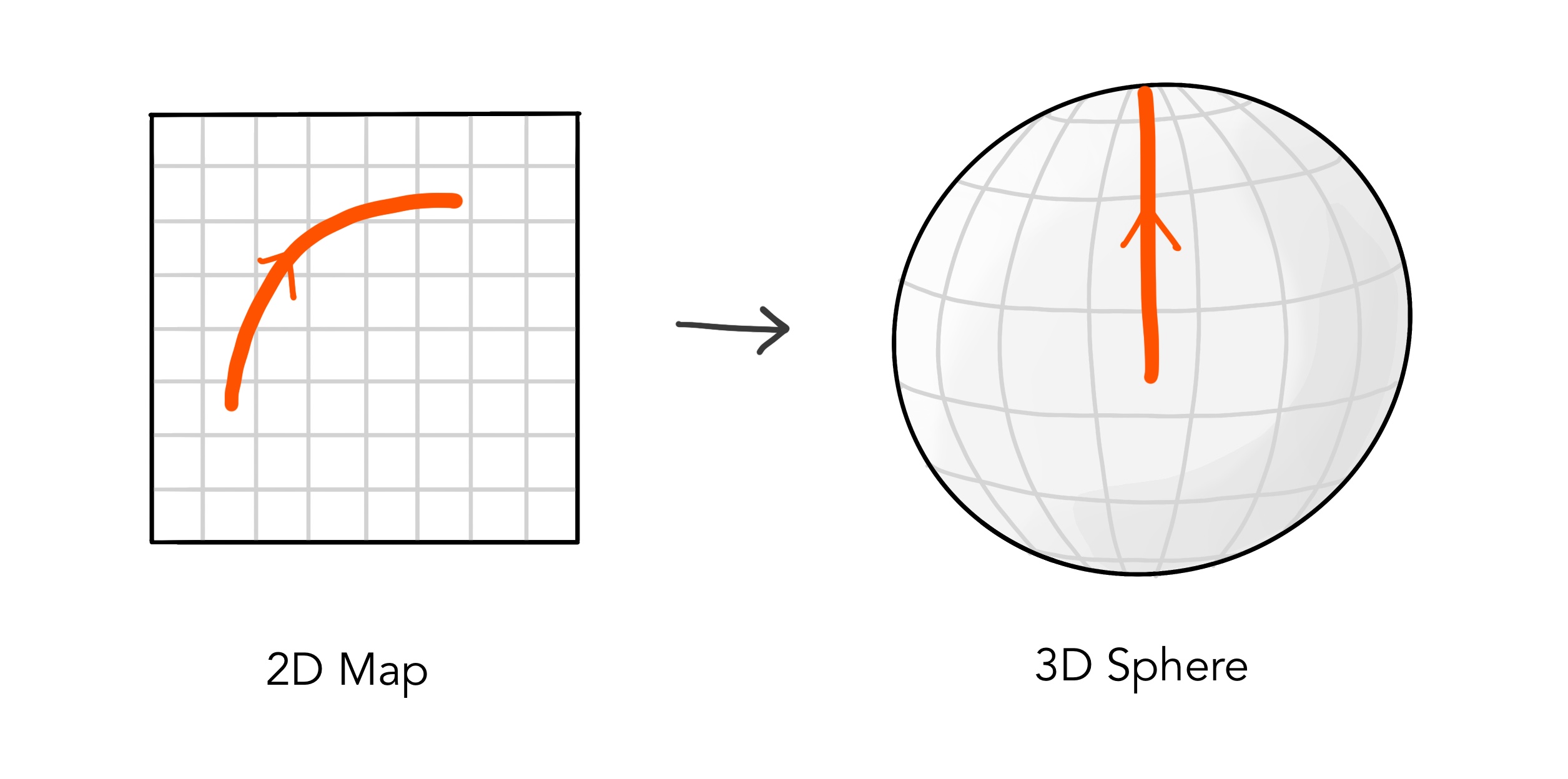
What is a straight line? Consider that we draw a straight line on a flat piece of paper (that’s 2 dimensional). Now, if we roll the paper
into 3 dimensions, the line isn’t straight anymore, rather curved.
Straight lines can become curved and vice versa when the number of dimensions change. Figure on the right shows how a straight line drawn on a 3 dimensional sphere appears curved when we flatten out the sphere onto 2 dimensions. Similarly, a line that’s straight in 4 dimensional spacetime might not be straight anymore when seen in 3 dimensions.
We know that accelerating bodies curve spacetime. We also know that acceleration can be substituted with gravitational field, since gravitational mass is equal to inertial mass. Since gravitational fields are caused by the presence of mass, we conclude that mass causes spacetime to curve. This curvature of spacetime in turn dictates the movement of mass in it. Thus, whenever a mass is present, spacetime cannot be Euclidean, but Gaussian (curved).
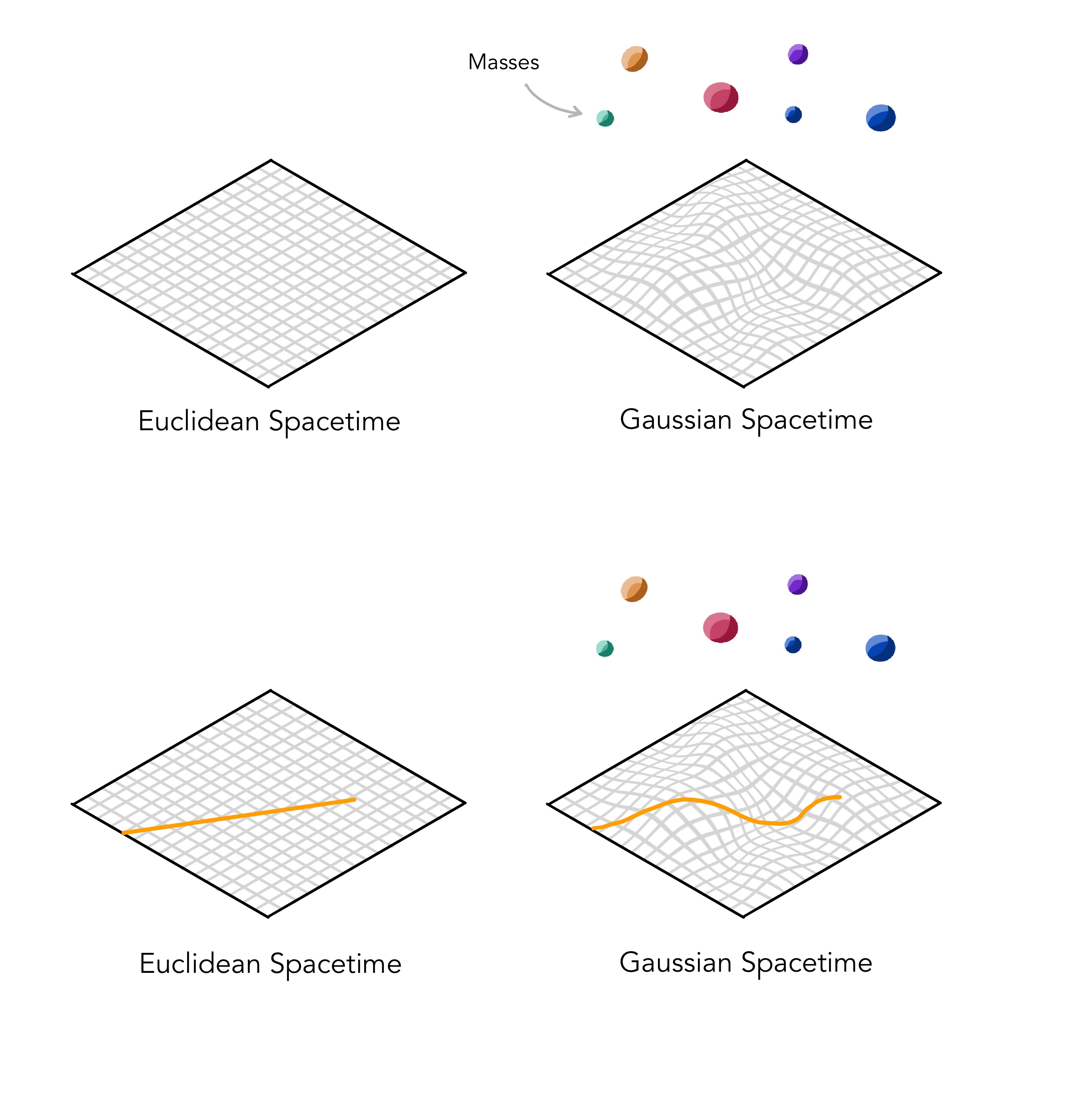
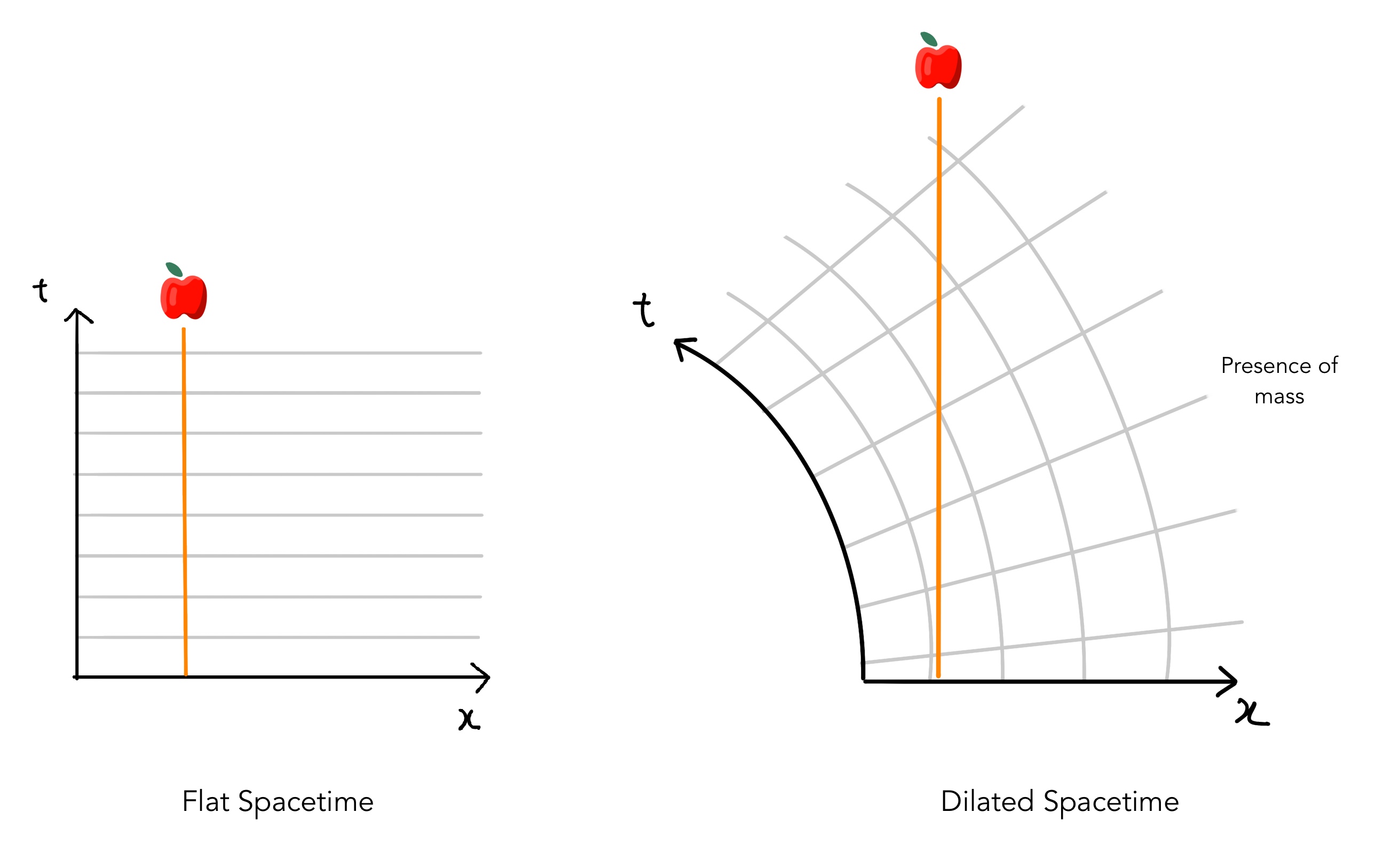
Consider the familiar 2D diagram with space on the X axis and time on the Y axis. Without the presence of any mass, spacetime is Euclidean, behaving like it used to in Special Relativity. Any stationary object, like an apple. would have a vertical worldline (the path it traces on the graph), as it is currently just moving through time.
Now, let’s place a massive object, like the earth, towards the right, which would cause spacetime to curve. More specifically, more the gravitational field, the slower time passes. This leads to the spacetime diagram getting distorted, with time passing more
slowly to the right. Now, if we make a worldline of an apple, it will still be straight, as
it was initially at rest and just moving through time. Notice however, due to spacetime now being curved, it has inevitably also moved along space (the X-coordinate), towards the right (towards the earth). This clearly shows the effect of gravity- Earth curves spacetime such that objects initially at rest start falling towards it. [3]
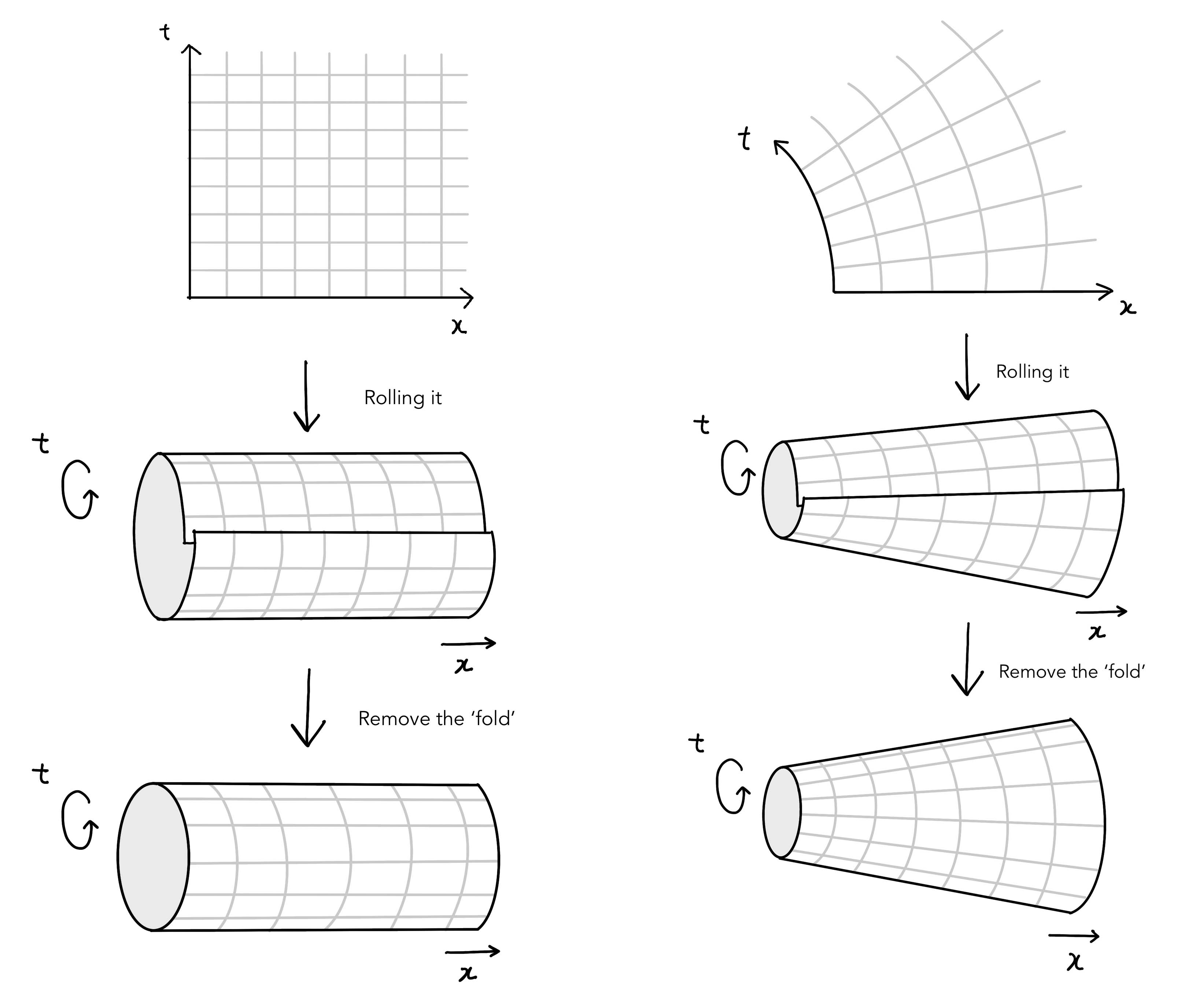
Curved spacetime on a flat surface can be difficult to visualise, even if we restrict ourselves to just one spatial dimension. Welcome embedding diagrams, which are simply rolled up versions of the 2D curved spacetime diagrams we just saw. Embedding diagrams help visualise the curvature in spacetime better and more intuitively. Remember that, although in 3D, embedding diagrams still only show one time dimension and one spatial dimension.
When one literally rolls a flat piece of paper, it results in a spiral fold rather than a continuous cylinder. The same is applicable here. An
object moving through time would not end up at the same point in the past after every revolution, but at a different point in the future.
We can however, for the sake of simplification, ignore this fold for our purposes, as it would serve to distract from the actual purpose of the
diagram.
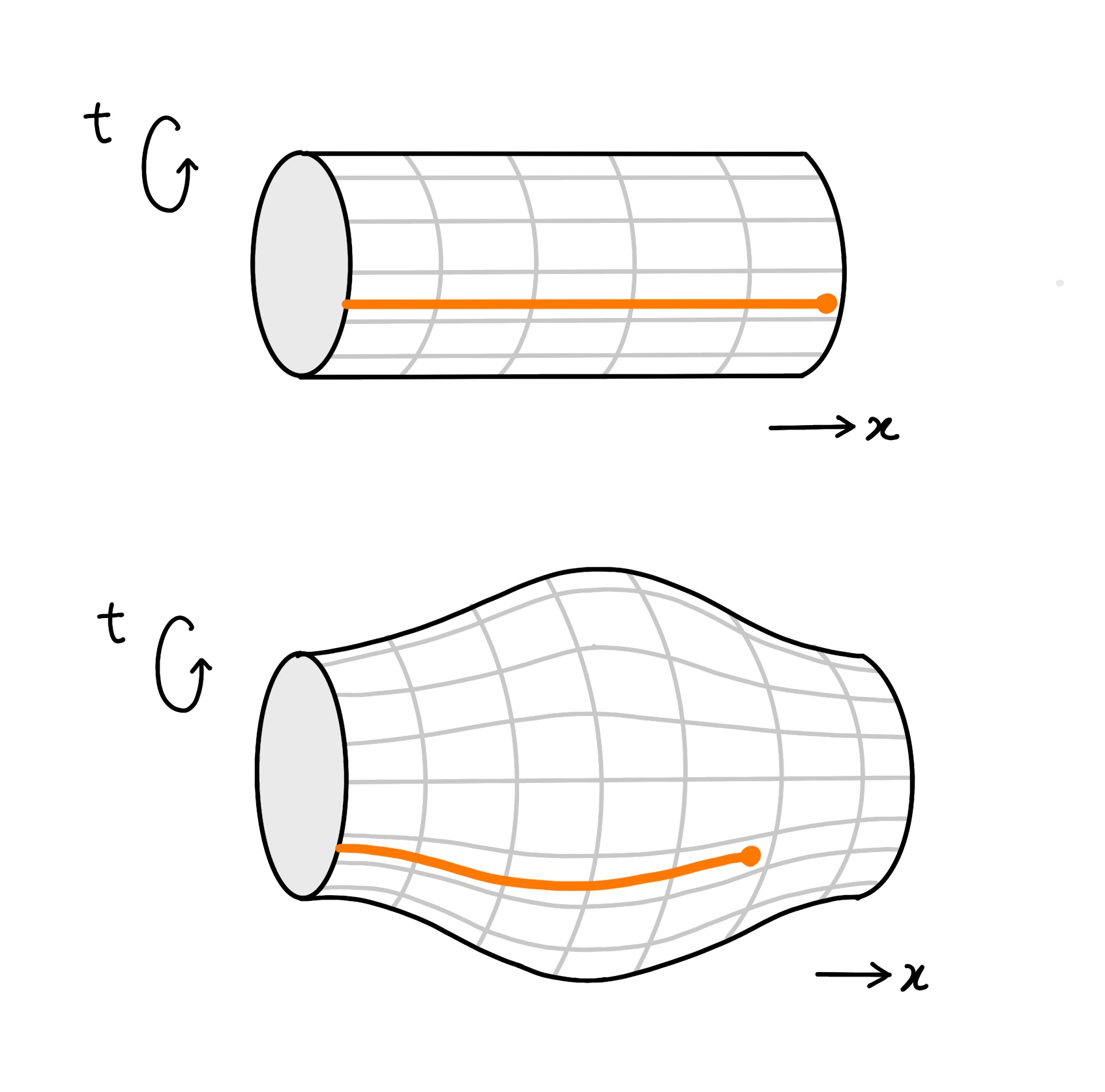
The visual on the right shows the worldline of an apple as it "falls" through curved spacetime under the influence of gravity. [4]
Press 'Play' to see the action. As time gets dilated on the right, the worldline starts drifting towards the right. This reflects in the movement of the apple in space, as it accelerates towards the right.
Consider the apple kept, initially stationary, at the leftmost point. Even while stationary, it is constantly passing through time, and its worldline forms loops around the embedding diagram. Now, try moving the slider to increase the time dilation towards the right. Due to the curvature of spacetime, the worldline starts drifting towards the right, ie. towards the supposed massive object causing the time dilation [5]. Thus, the apple starts “falling” due to the “force” of gravity.
Note that different types of embedding diagrams can be made depending on the calculations. The time dilation can be shown as a bulge (called dual metric) or as a crunch (called absolute metric). [6]
How do stronger gravitational fields visually affect embedding diagrams?
Consider a massive body as shown on the right. Let's start by giving it the mass and radius of our sun. The central bulge in the embedding diagram below it shows how the gravitational field of the sun dilates time, and it is bigger for more massive bodies. This type of embedding diagram is called a Dual Embedding.
As you'd increase the mass, notice the dotted circle around the object. That's called the Schwarzschild Radius. When an object’s radius becomes smaller than its Schwarzschild Radius, it turns into a black hole.
Notice the black hole embedding. The graph outside the event horizon familiarly shows space on the X axis and time on the Y axis. Approaching the event horizon, the embedding isn't really well defined. However, once inside the event horizon, space and time get interchanged. Time lies on the X axis. Thus, once inside the event horizon, the singularity lies in your future. The journey is inevitable.
Since light is massless and travels at c, it doesn’t move through time, and only through space (remember the speedometer diagram).
The visual shows light moving horizontally, just through space, both in the absence and presence of a gravitational field. Notice how light has to travel a larger distance in the curved spacetime diagram than the one which
is flat, in an equal amount of time. This means that the presence of mass, apart from dilating time, must also be expanding space.
We know that masses slow down time. We also know that masses increase space.Move the slider here to see how both of them are affected, as the mass of an object increases.
The top embedding shows the familiar spacetime diagram, with time on the Y axis (rolled up), and space along the X axis. The bottom diagram is a space-space diagram, with both the X and Y axes showing spatial directions [7].
Point to remember is that all these are abstract visualizations which help develop intuition, and in no way are visual representations of how
curved spacetime literally looks like.
An observable implication of spacetime curvature is the curving of light. Note that the velocity of light (its speed and direction) are still constant. It is the spacetime itself that curves around it, making it look curved to an outside observer.
As light just passes through space and not through time, we can use the space-space diagram (the bottom one above) to make a path for light. We can tell intuitively that curved spacetime causes the beam of light to bend towards the mass [7].
It is impossible to visualise or even conceive of how 4 dimensional spacetime truly behaves. We can, however, extract dimensions and develop abstractions that allow us to fit in our observations of the real world as much as possible. Embedding diagrams are one such way of abstraction and representation of something that's not only weirder than you imagine, it's weirder than you can imagine.